محاسبه فاصله اطمینان در مایکروسافت اکسل

یکی از روش های حل مسائل آماری، محاسبه فاصله اطمینان است. این روش به عنوان نقطه برآورد مطلوب جایگزین با اندازه نمونه کوچک مورد استفاده قرار می گیرد. لازم به ذکر است که روند محاسبه فاصله اطمینان خود بسیار پیچیده است. اما ابزار برنامه اکسل آن را تا حدودی ساده تر می کند. بیایید دریابیم که چگونه در عمل انجام می شود.

همچنین ببینید: توابع آماری در اکسل

روش محاسبه

این روش برای تخمینی فاصله از مقادیر مختلف آماری استفاده می شود. وظیفه اصلی این محاسبه خلاص شدن از عدم اطمینان تخمین نقطه است.

در اکسل دو روش اصلی برای انجام محاسبات با استفاده از این روش وجود دارد: زمانی که واریانس شناخته شده است و زمانی که ناشناخته است. در مورد اول، عملکرد CONFIDENCE.NORM برای محاسبات استفاده می شود، و در مورد دوم ، DETERMIT.SUDENT .

روش 1: عملکرد CONFIDENCE.NORM

اپراتور CONFIDENCE.NORM ، متعلق به گروه آماری توابع، ابتدا در اکسل 2010 ظاهر شد. در نسخه های قبلی این برنامه، CONFIDENCE آنالوگ استفاده می شود . وظیفه این اپراتور محاسبه فاصله اطمینان با توزیع نرمال برای جمعیت متوسط ​​است.

نحو آن به شرح زیر است:

=ДОВЕРИТ.НОРМ(альфа;стандартное_откл;размер)

آلفا یک استدلال است که نشان دهنده سطح اهمیت است که برای محاسبه سطح اطمینان استفاده می شود. سطح اطمینان عبارت زیر است:

(1-«Альфа»)*100

"انحراف استاندارد" یک استدلال است که ماهیت آن از نام مشخص است. این انحراف معیار نمونه پیشنهادی است.

"اندازه" یک استدلال است که اندازه نمونه را تعیین می کند.

تمام استدلال های این اپراتور مورد نیاز است.

تابع TRUST دقیقا همان استدلال و امکانات را همانند یک قبلی دارد. نحو آن:

=ДОВЕРИТ(альфа;стандартное_откл;размер)

همانطور که می بینید، تفاوت فقط به نام اپراتور است. این تابع برای سازگاری در اکسل 2010 و در نسخه های جدیدتر در رده ویژه «سازگاری» باقی مانده است . در نسخه های اکسل 2007 و قبل از آن، در گروه اصلی اپراتورهای آماری قرار دارد.

مرز فاصله اطمینان با استفاده از فرمول زیر تعیین می شود:

X+(-)ДОВЕРИТ.НОРМ

جایی که X میانگین مقدار نمونه است که در وسط محدوده انتخاب شده واقع شده است.

حالا بیایید به چگونگی محاسبه فاصله اطمینان در یک مثال خاص نگاه کنیم. 12 آزمایش انجام شد که نتیجه آن نتایج مختلف ذکر شده در جدول بدست آمد. این کلیت ماست. انحراف معیار 8 است. ما باید یک فاصله اطمینان را در سطح اطمینان 97٪ محاسبه کنیم.

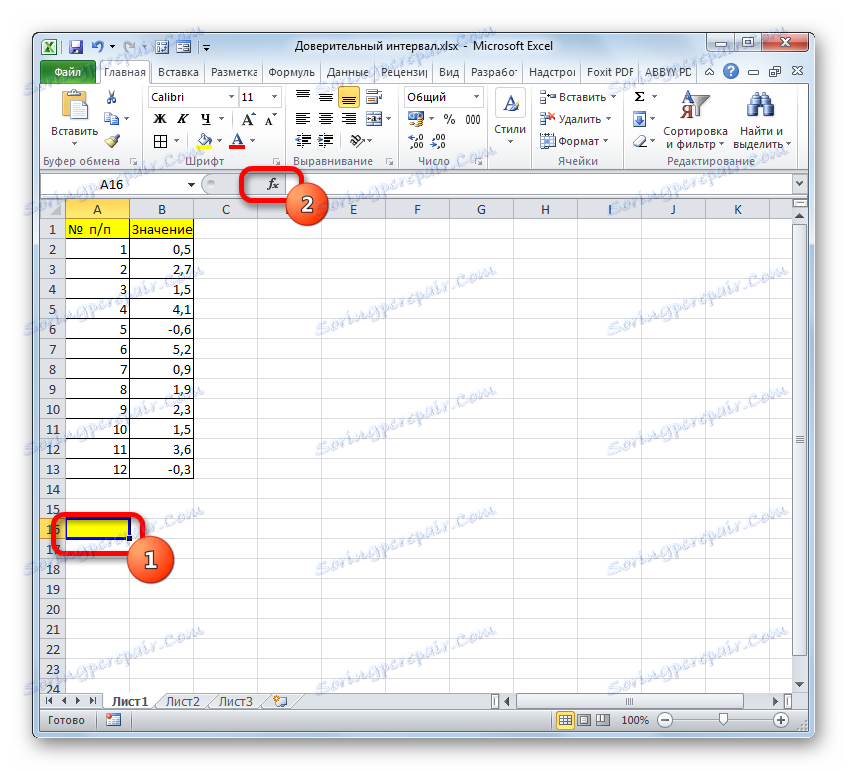
1. سلول را انتخاب کنید که در آن نتیجه پردازش داده نمایش داده می شود. بر روی دکمه "درج تابع" کلیک کنید .
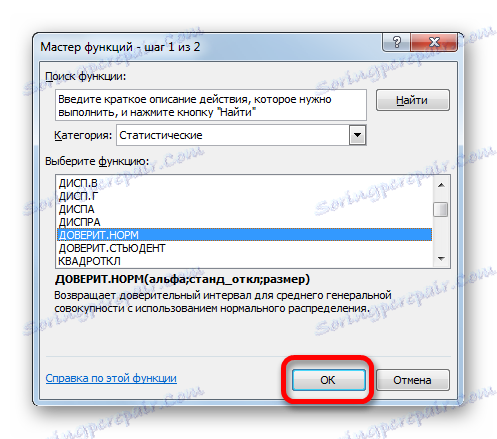
2. جادوگر تابع ظاهر می شود. به رده "آماری" بروید و نام "TRUST . NORM" را انتخاب کنید . پس از آن ما بر روی دکمه "OK" کلیک کنید.
3. پنجره بحث باز می شود. زمینه های آن به طور طبیعی با نام استدلال مطابقت دارد.
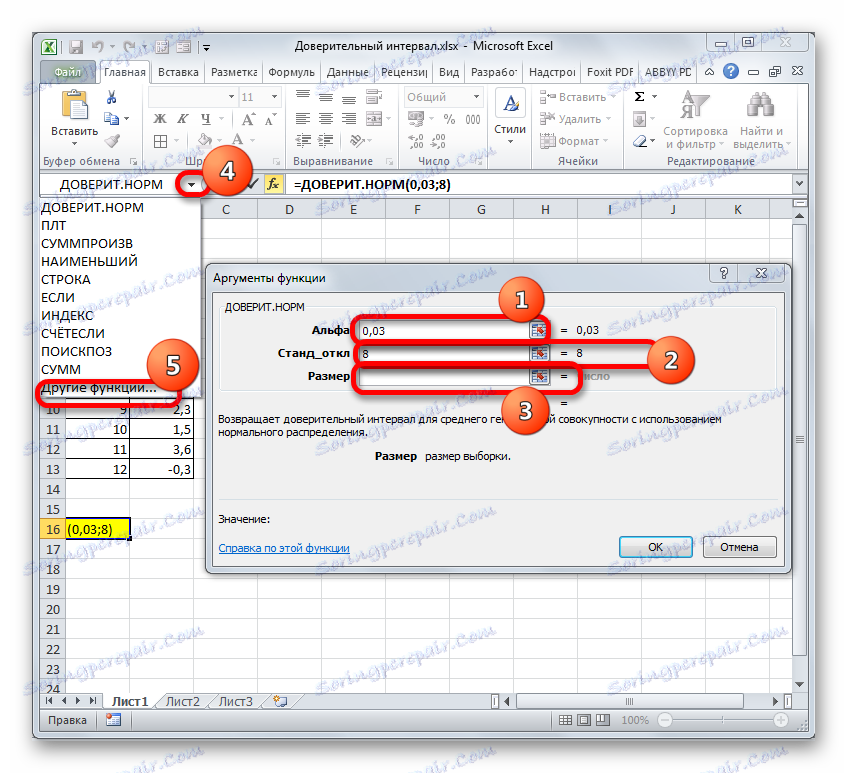
   مکان نما را در قسمت اول تنظیم کنید - "آلفا" . در اینجا باید سطح اهمیت را مشخص کنیم. به یاد داشته باشید، سطح اعتماد ما 97٪ است. در همان زمان، ما گفتیم که به روش زیر محاسبه می شود:

   (1-«Альфа»)*100

   بنابراین، برای محاسبه سطح اهمیت، یعنی، برای تعیین مقدار "آلفا" باید فرمول فرم زیر را اعمال کنید:

   (1-уровень доверия)/100

   به این معناست که ارزش را جایگزین می کنیم:

   (1-97)/100

   با محاسبات ساده، متوجه می شویم که استدلال "آلفا" 0.03 است . این مقدار را در فیلد وارد کنید

   همانطور که می دانید، شرایط انحراف استاندارد 8 است . بنابراين، در بخش "انحراف استاندارد" به سادگی اين عدد را بنویسيد.

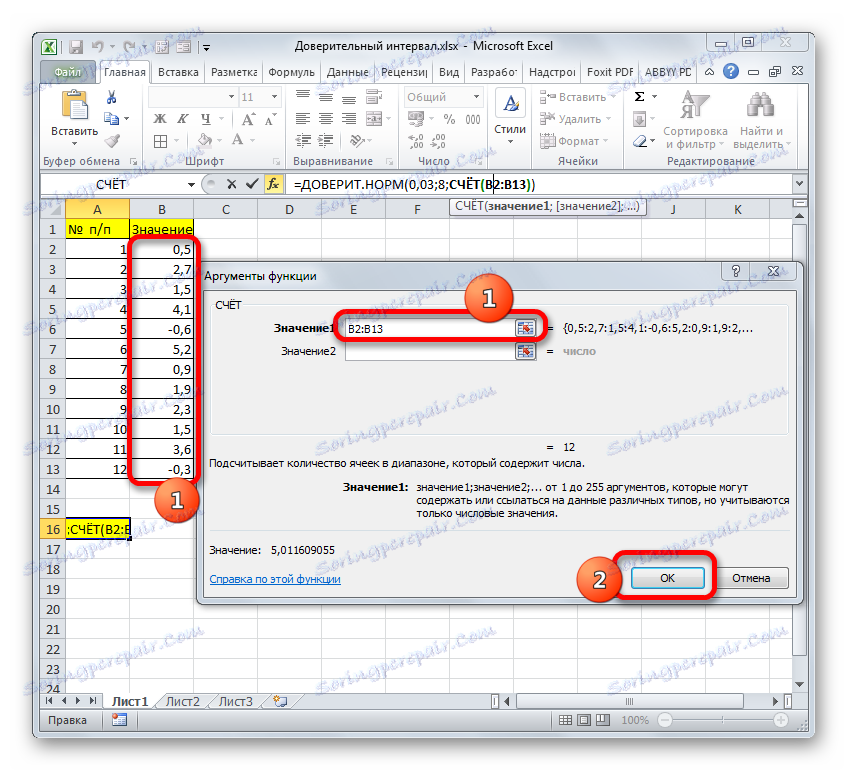
   در قسمت "Size" شما باید تعداد عناصر تست های انجام شده را وارد کنید. به یاد داشته باشید، 12 مورد از آنها وجود دارد. اما برای این که فرمول را به صورت خودکار بسازیم و آن را هر بار که یک تست جدید انجام می شود ویرایش کنیم، این مقدار را با عدد معمولی تعیین می کنیم، اما با استفاده از عملگر COUNT . بنابراین، مکان نما را در قسمت «اندازه» قرار دهید، سپس روی مثلثی که در سمت چپ نوار فرمول قرار دارد کلیک کنید.

   یک لیست از توابع اخیرا استفاده شده به نظر می رسد. اگر اخیرا توسط شما از اپراتور ACCOUN استفاده شد، باید در این فهرست باشد. در این مورد، شما فقط باید بر روی نام آن کلیک کنید. در صورت مخالفت، اگر شما آن را پیدا نکنید، سپس از طریق آیتم "سایر توابع ..." بروید .

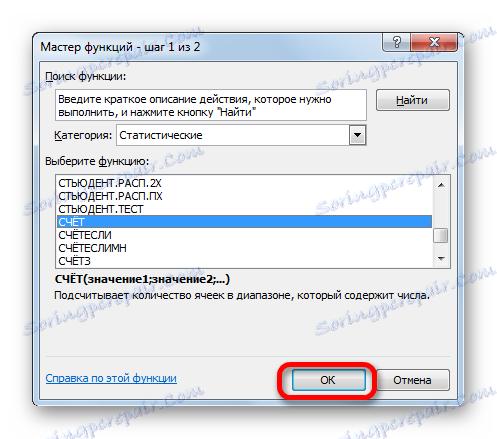
4. استاد توابع، که قبلا به ما آشناست، ظاهر می شود . ما دوباره به گروه آماری حرکت می کنیم. نام "ACCOUNT" را در آنجا انتخاب کنید روی دکمه OK کلیک کنید.
5. پنجره argument از عبارت فوق بیان می شود. این تابع برای محاسبه تعداد سلول ها در محدوده مشخص شده که دارای مقادیر عددی هستند طراحی شده است. نحو آن به شرح زیر است:

   =СЧЁТ(значение1;значение2;…)

   گروه استدلال "ارزش ها" مرجع محدوده ای است که در آن شما نیاز به محاسبه تعداد سلول های پر شده با داده های عددی را دارید. در کل می توان تا 255 چنین استدلال هایی داشته باشد، اما در مورد ما فقط یک مورد نیاز است.

   مکان را در فیلد "Value1" قرار دهید و با نگه داشتن دکمه سمت چپ ماوس، دامنه ای را که شامل مجموعه ما در ورق است را انتخاب کنید. سپس آدرس او در این زمینه نمایش داده خواهد شد. روی دکمه OK کلیک کنید.

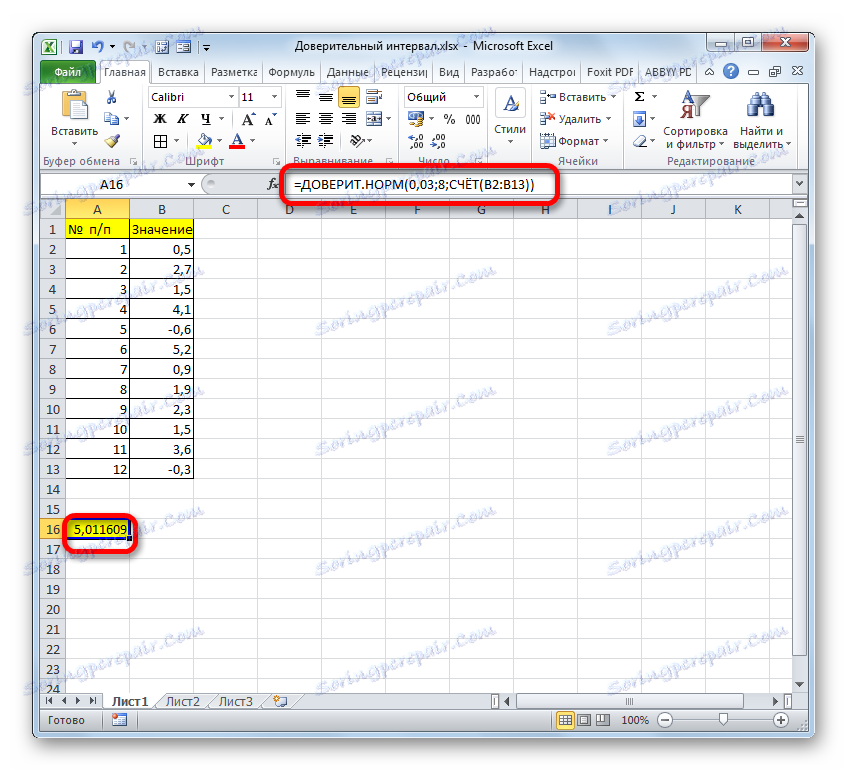
6. پس از آن، برنامه محاسبات را انجام می دهد و نتیجه را در سلولی که در آن واقع شده است نمایش می دهد. در مورد خاص ما، فرمول به شکل زیر بود:

   =ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))

   نتیجه کلی محاسبات 5،011،609 بود.

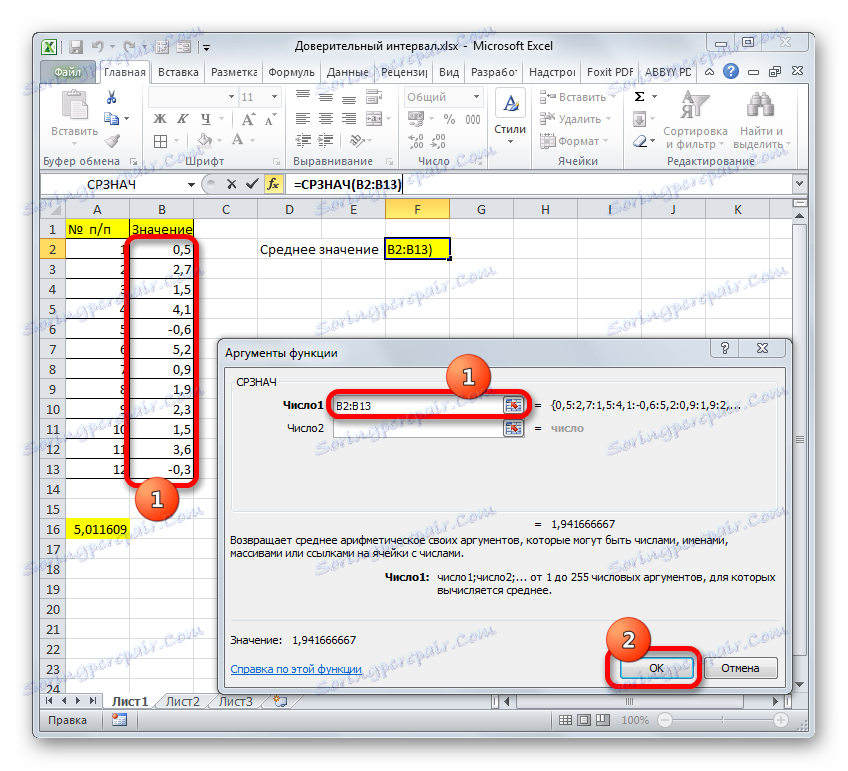
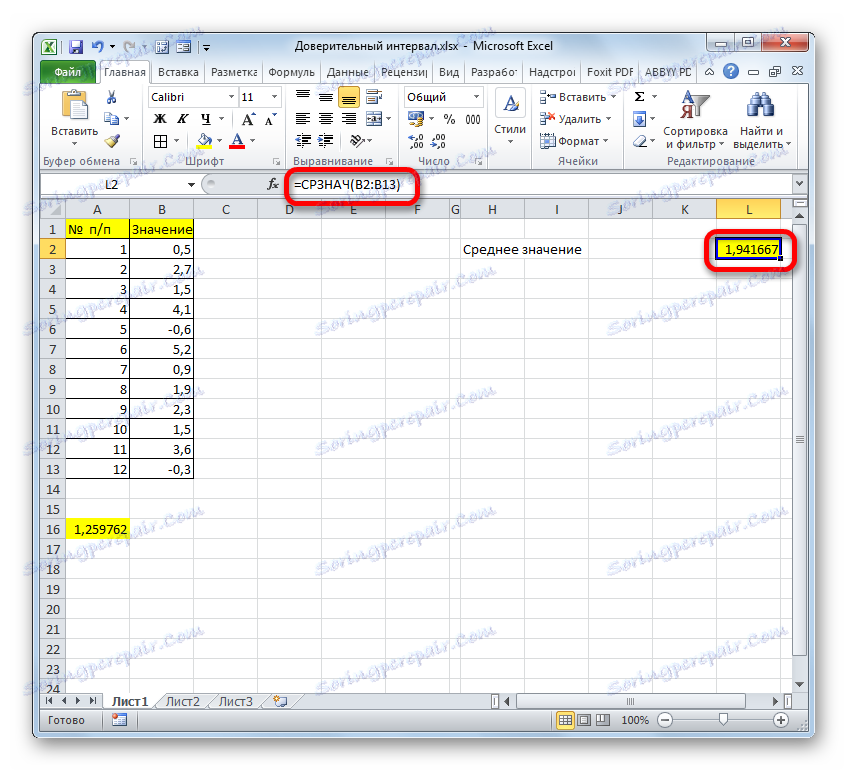
7. اما این همه نیست همانطور که ما یاد می گیریم، محدودیت فاصله اطمینان با اضافه کردن و تفریق از میانگین مقدار نمونه محاسبه CONFIDENCE.NORM محاسبه می شود. به این ترتیب، محدودیت راست و چپ فاصله اطمینان به ترتیب محاسبه می شود. میانگین مقدار نمونه خود را می توان با استفاده از اپراتور AVERAGE SYSTEM محاسبه کرد.

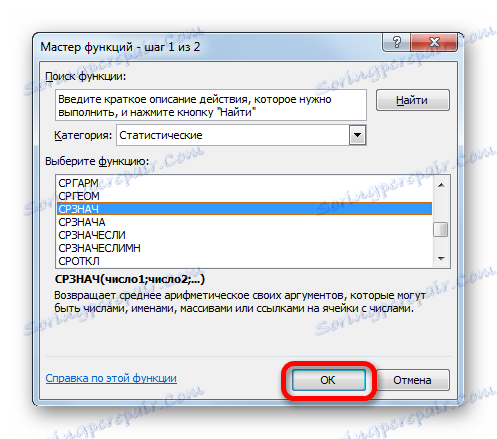
   این اپراتور برای محاسبه میانگین ریاضی محدوده انتخاب شده از اعداد طراحی شده است. این نحو نسبتا ساده ای دارد:

   =СРЗНАЧ(число1;число2;…)

   استدلال "شماره" می تواند یک مقدار عددی جداگانه باشد، یا یک مرجع به سلول، یا حتی محدوده عدد صحیح که حاوی آنها است.

   بنابراین، سلول را انتخاب کنید که در آن محاسبه مقدار متوسط ​​نمایش داده می شود و بر روی دکمه "Insert function" کلیک کنید.

8. جادوگر تابع باز می شود. باز هم به رده "آماری" بروید و از لیست "نامحدود" را انتخاب کنید . همانطور که همیشه، ما بر روی دکمه "OK" کلیک کنید.
9. پنجره بحث شروع می شود. مکان نما را در قسمت "شماره 1" قرار دهید و دکمه سمت چپ ماوس را فشار دهید تا کل محدوده مقادیر را انتخاب کنید. پس از اینکه مختصات در قسمت نمایش داده می شود، بر روی دکمه OK کلیک کنید.
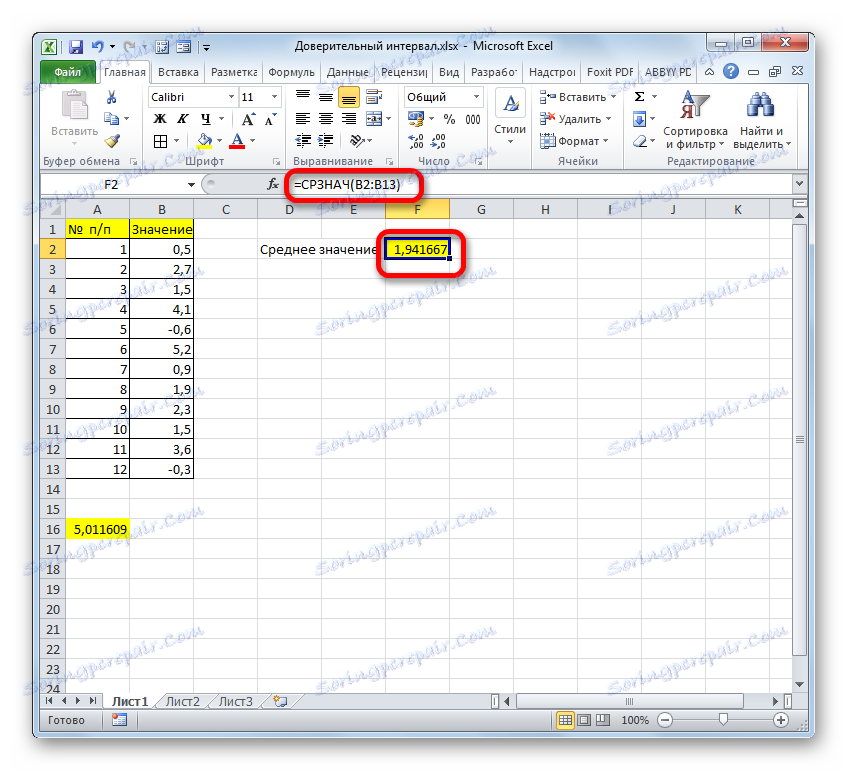
10. بعد از این، AVERAGE نتیجه محاسبات را به مورد ورق مقایسه می کند .
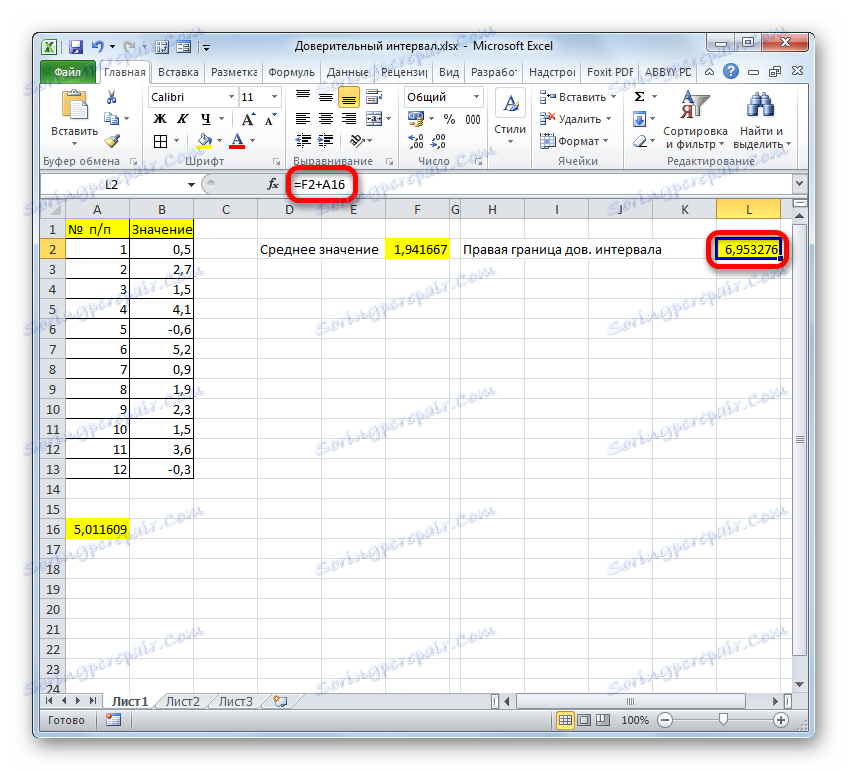
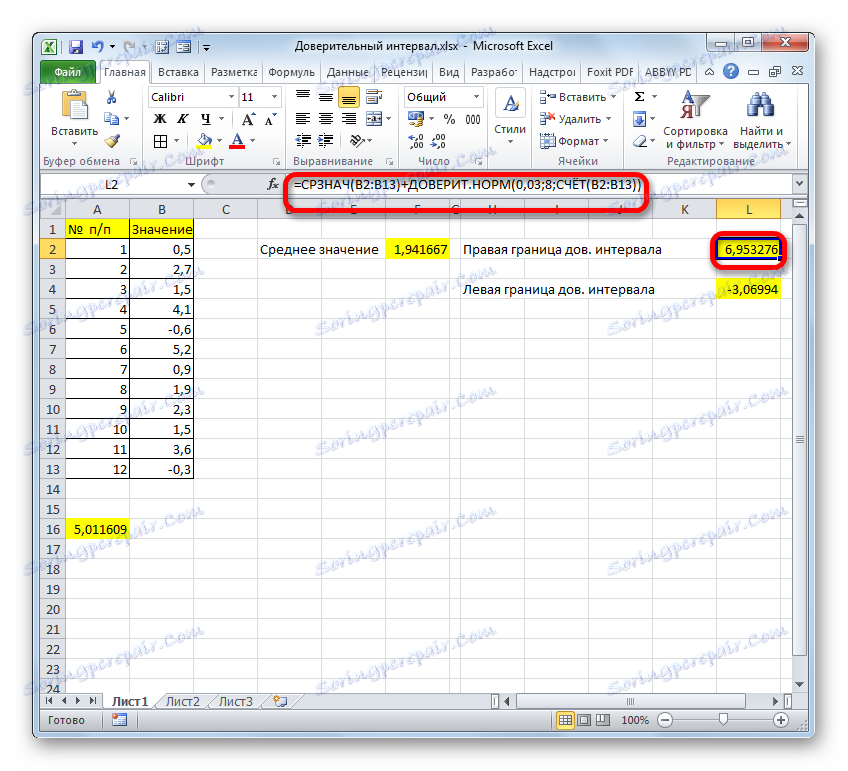
11. ما مرز راست فاصله اطمینان را محاسبه می کنیم. برای انجام این کار، یک سلول جداگانه را انتخاب کنید، علامت "=" را قرار دهید و محتویات عناصر ورق را اضافه کنید، که در آن نتایج محاسبات توابع AVERAGE و CONFIDENCE.NORM قرار گرفته است . برای انجام محاسبات، بر روی کلید Enter کلیک کنید . در مورد ما فرمول زیر را دریافت کردیم:

    =F2+A16

    نتیجه محاسبه: 6،953276

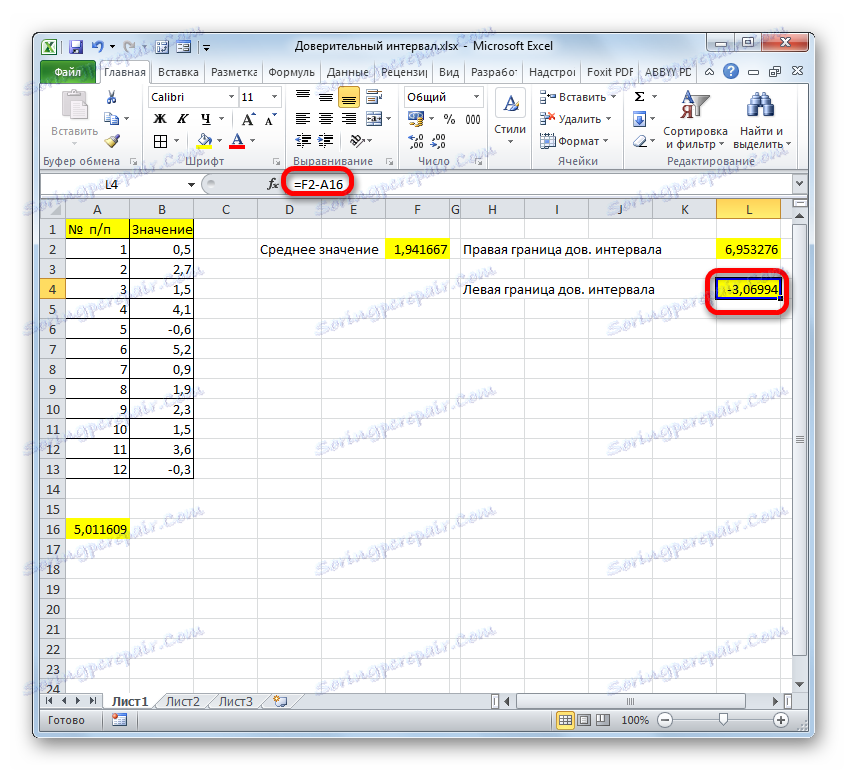
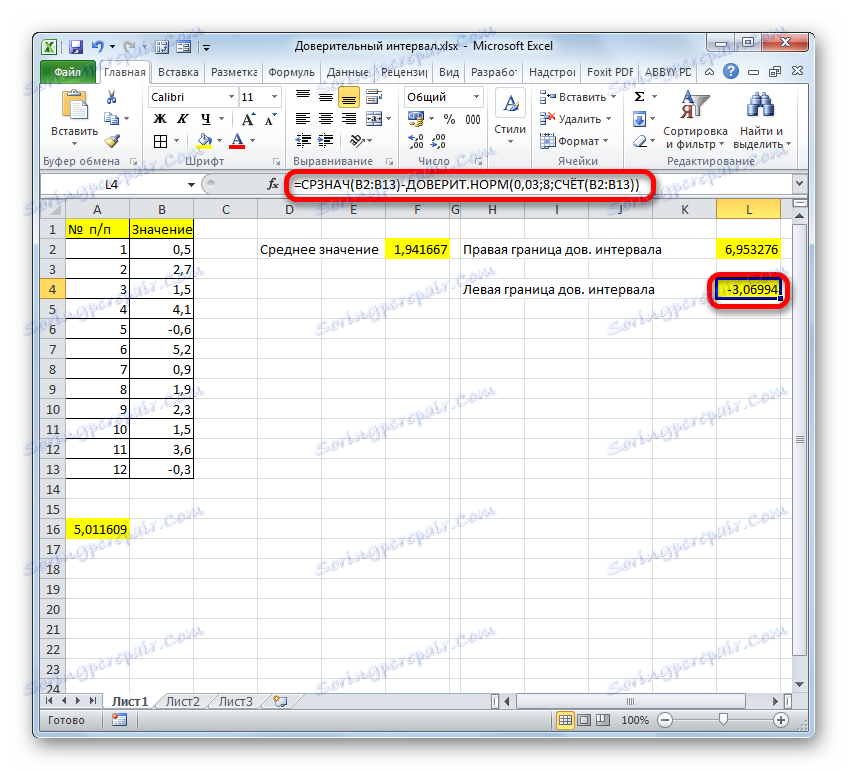
12. به همین ترتیب، مرز چپ محدوده اطمینان را محاسبه می کنیم، فقط این بار نتیجه محاسبات OPF CONFIDENCE.NORM را از نتیجه محاسبه محدوده محاسبه می کنیم. این فرمول برای مثال ما از نوع زیر است:

    =F2-A16

    نتیجه محاسبه: -3،06994

13. ما سعی کردیم تمام مراحل محاسبه فاصله اطمینان را به طور دقیق توضیح دهیم، بنابراین ما هر فرمول را به تفصیل شرح دادیم. اما تمام اقدامات را می توان در یک فرمول ترکیب کرد. محاسبه مرز راست فاصله اطمینان می تواند به صورت زیر باشد:

    =СРЗНАЧ(B2:B13)+ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))

14. محاسبه مشابهی از مرز چپ به صورت زیر است:

    =СРЗНАЧ(B2:B13)-ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))

روش 2: عملکرد TREST FESTUDENT

علاوه بر این، در Excel، یک تابع دیگر وجود دارد که با محاسبه فاصله اطمینان - DETERMIT.SUDENT مرتبط است . این فقط از اکسل 2010 آغاز می شود. این اپراتور محاسبه فاصله اطمینان جمعیت کل را با استفاده از توزیع دانش آموز انجام می دهد. این بسیار راحت است که از آن در مواردی استفاده شود که واریانس و در نتیجه انحراف استاندارد ناشناخته باشد. نحو عملگر عبارت است از:

=ДОВЕРИТ.СТЬЮДЕНТ(альфа;стандартное_откл;размер)

همانطور که می بینید، نام اپراتورها در این مورد بدون تغییر باقی ماند.

بیایید ببینیم چگونه محدوده فاصله اطمینان را با یک انحراف استاندارد ناشناخته محاسبه می کنیم با استفاده از مثال همان مجموعه ای که در روش قبلی در نظر گرفتیم. سطح اعتماد، مانند گذشته، 97٪ را دریافت می کند.

1. سلول را انتخاب کنید که در آن محاسبه انجام خواهد شد. بر روی دکمه "درج تابع" کلیک کنید .
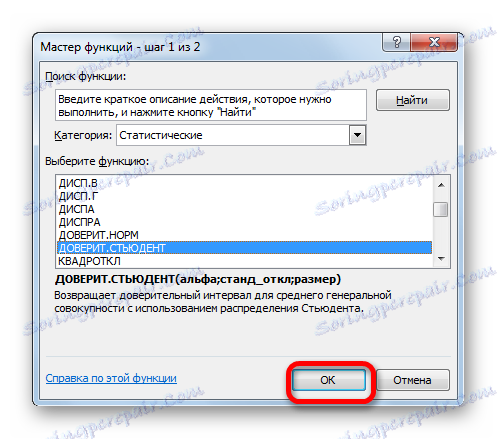
2. در جادوگر تابع که باز می شود، به بخش "آماری" بروید . نام "STUDENT TRUSTED" را انتخاب کنید. روی دکمه OK کلیک کنید.
3. پنجره استدلال اپراتور مشخص شده راه اندازی شده است.

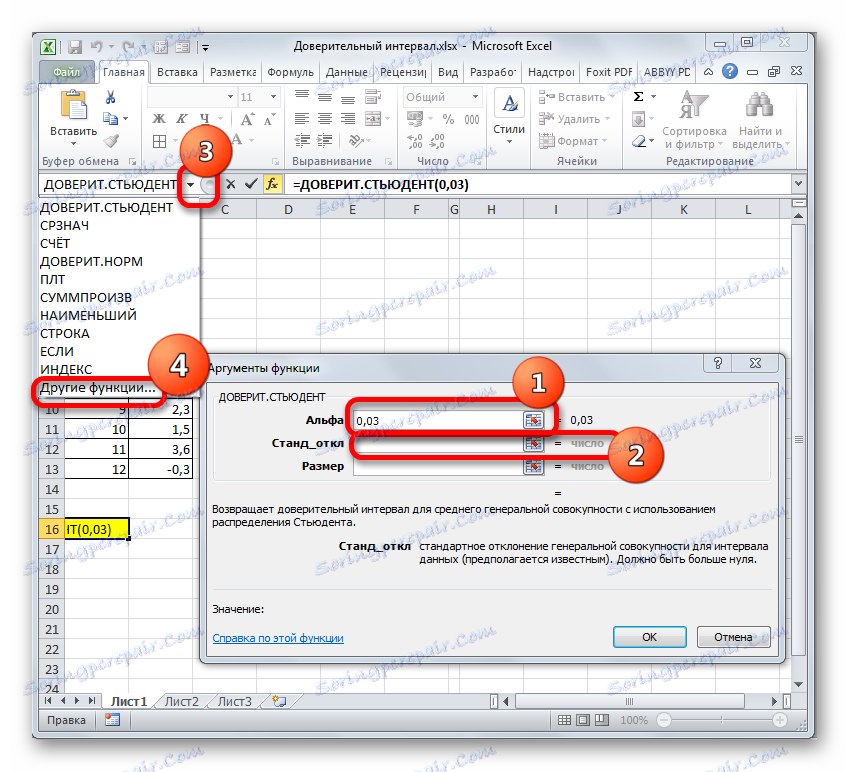
   در فیلد "آلفا" ، با توجه به اینکه سطح اعتماد 97٪ است، شماره 0.03 را بنویسید. بار دوم در اصول محاسبه این پارامتر متوقف نخواهد شد.

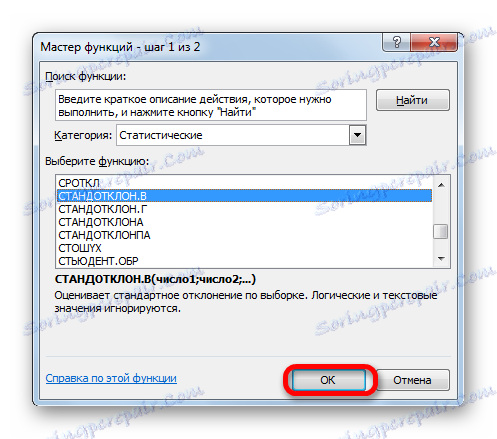
   پس از آن مکاننما را در قسمت «انحراف استاندارد» قرار دهید. در این زمان، این رقم برای ما ناشناخته است و لازم است محاسبه شود. این کار با کمک یک تابع خاص انجام می شود - STANDOWCLON.V . برای تماس با پنجره این اپراتور، روی مثلث سمت چپ نوار فرمول کلیک کنید. اگر در لیست باز شده نام نامی را پیدا نکنیم، سپس زیر مورد "سایر توابع ..." بروید .

4. جادوگر تابع شروع می شود. رفتن به رده "آماری" و در آن نام "STANDOWCLON.V" را یادداشت کنید . سپس بر روی دکمه "OK" کلیک کنید.
5. پنجره بحث باز می شود. وظیفه اپراتور STANDOWCLONE B تعیین انحراف استاندارد نمونه است. نحو آن:

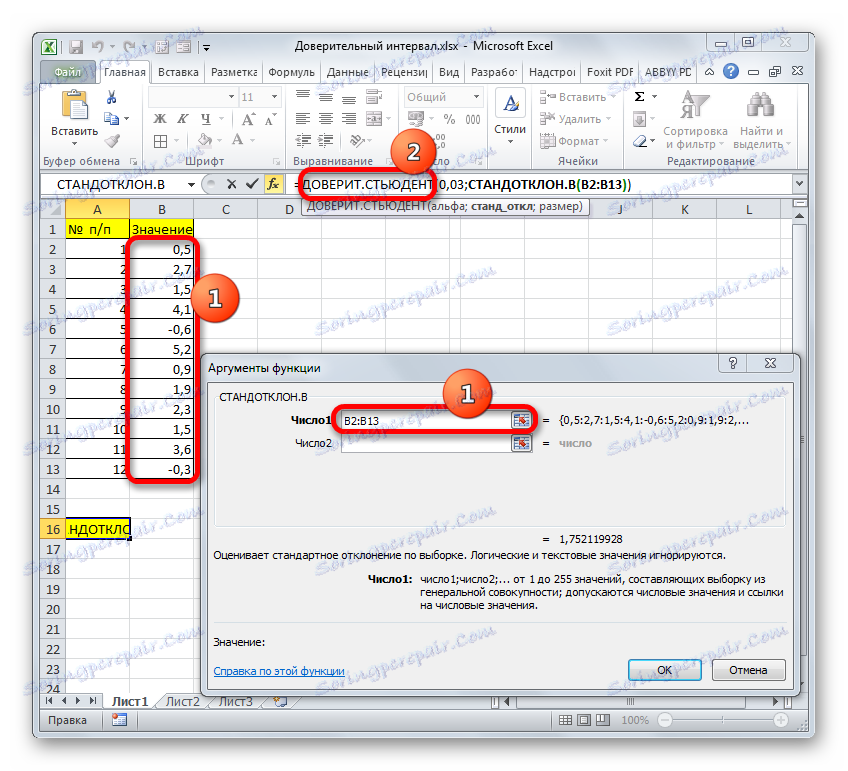
   =СТАНДОТКЛОН.В(число1;число2;…)

   دشوار است حدس بزنید که استدلال "شماره" آدرس عنصر انتخاب است. اگر نمونه در یک آرایه قرار داده شود، می توانید با استفاده از تنها یک استدلال، یک پیوند را به این محدوده بدهید.

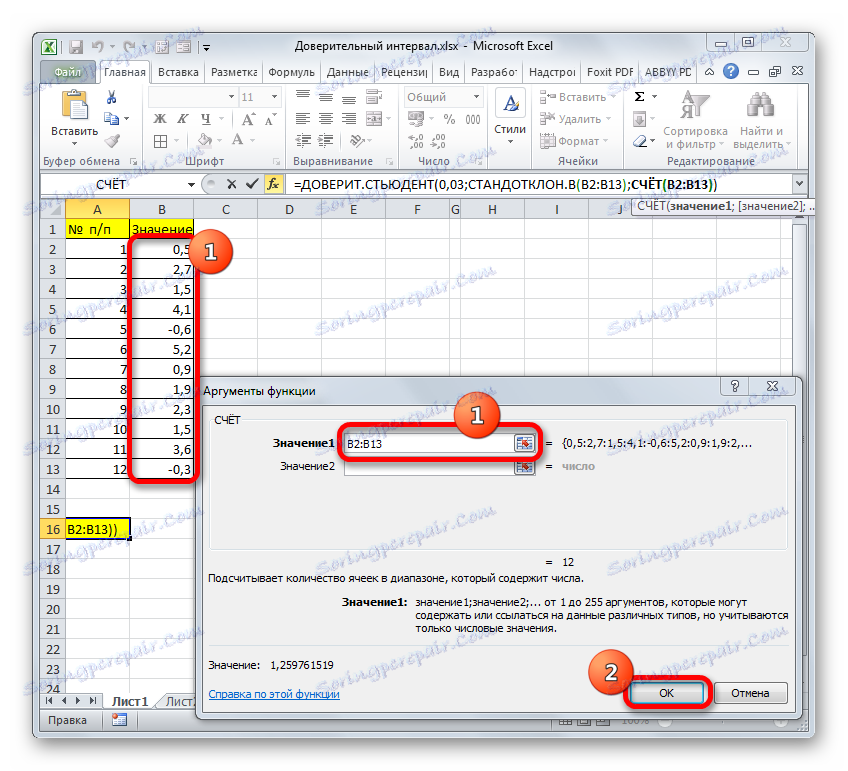
   ما مکان نما را در قسمت "Number1" قرار داده ایم و، همانطور که همیشه، نگه داشتن دکمه سمت چپ ماوس، مجموعه را انتخاب کنید. پس از اینکه مختصات در این زمینه هستند، عجله نکنید تا دکمه «OK» را فشار دهید، زیرا نتیجه نادرست خواهد بود. ابتدا ما باید به پنجره استدلال عملگر CONFIDENT STUDENT بازگردیم تا آخرین بحث را بیان کنیم. برای انجام این کار، روی نام مناسب در نوار فرمول کلیک کنید.

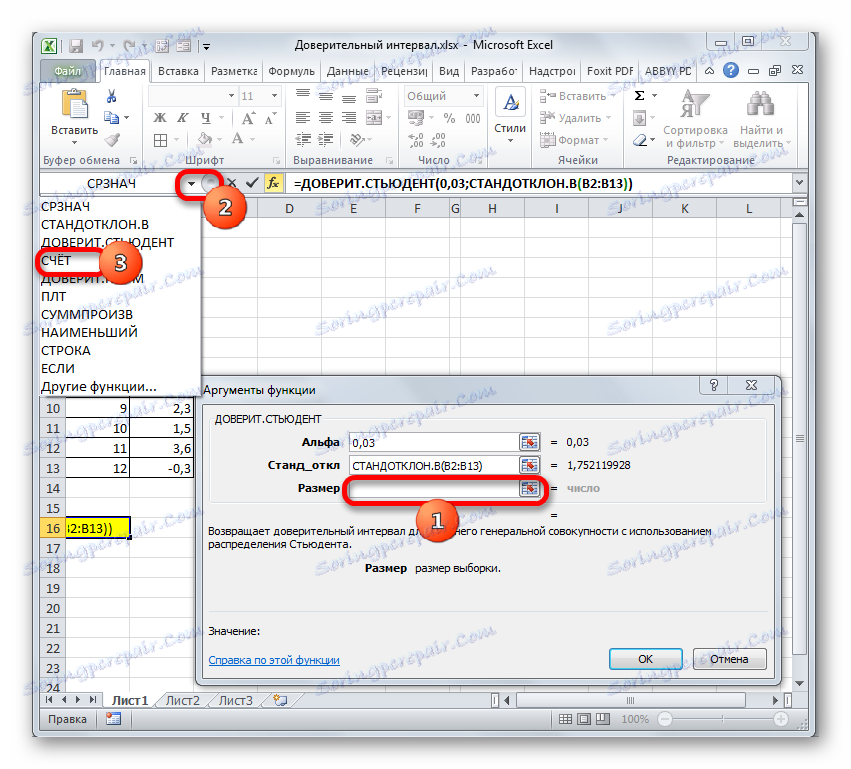
6. پنجره استدلال تابع آشنا دوباره باز می شود. مکان نما را در "اندازه" تنظیم کنید . دوباره بر روی مثلث که قبلا آشنا شده اید کلیک کنید تا به انتخاب اپراتورها بروید. همانطور که می دانید، ما به نام "ACCOUNT" نیاز داریم. از آنجایی که ما از این تابع در محاسبات در روش قبلی استفاده کردیم، در لیست موجود است، بنابراین فقط روی آن کلیک کنید. اگر شما آن را پیدا نکنید، سپس با توجه به الگوریتم توضیح داده شده در روش اول ادامه دهید.
7. هنگامی که در پنجره استدلال ACCOUNT قرار می گیرد، ما مکان را در فیلد "Number1" قرار می دهیم و دکمه ماوس را پایین نگه می دارد، جمعیت را انتخاب کنید . سپس بر روی دکمه "OK" کلیک کنید.
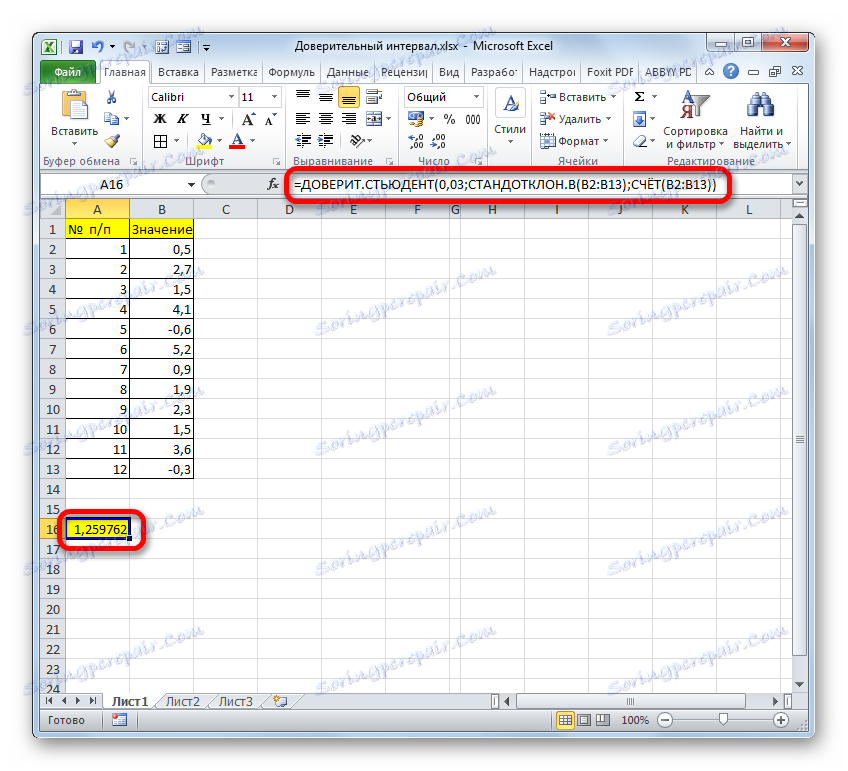
8. پس از آن، برنامه محاسبه و نمایش فاصله اطمینان را نشان می دهد.
9. برای تعیین مرزها، مجددا نیاز به محاسبه مقدار متوسط ​​نمونه است. اما با توجه به این که الگوریتم محاسبه با استفاده از فرمول AVERAGE همان روش قبلی است و حتی نتیجه تغییری نداشته است، ما در این مورد به طور مرتب دو بار دیگر به آن توجه نمی کنیم.
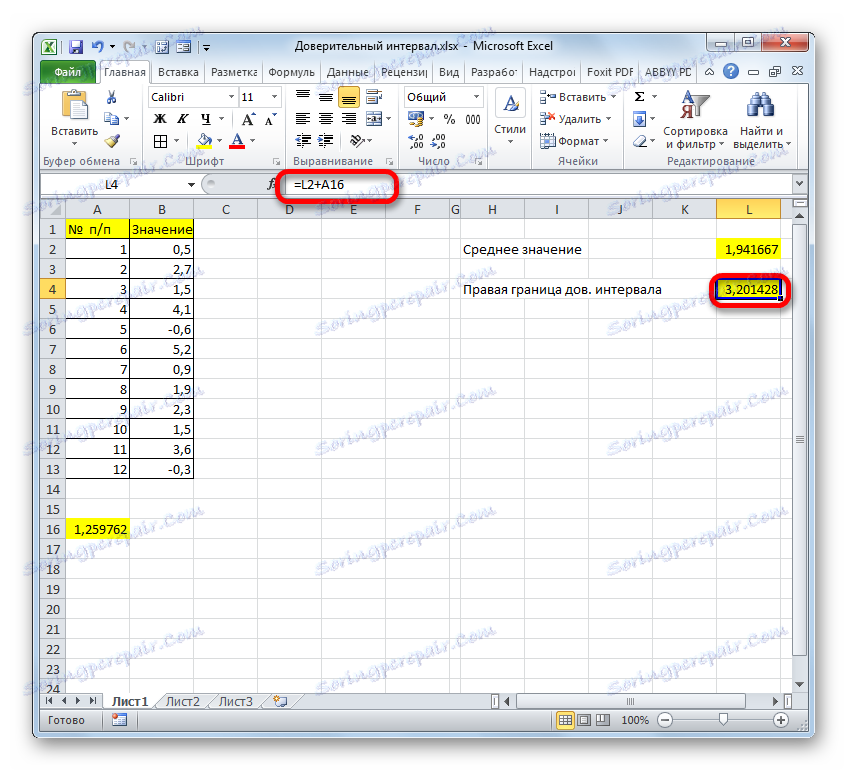
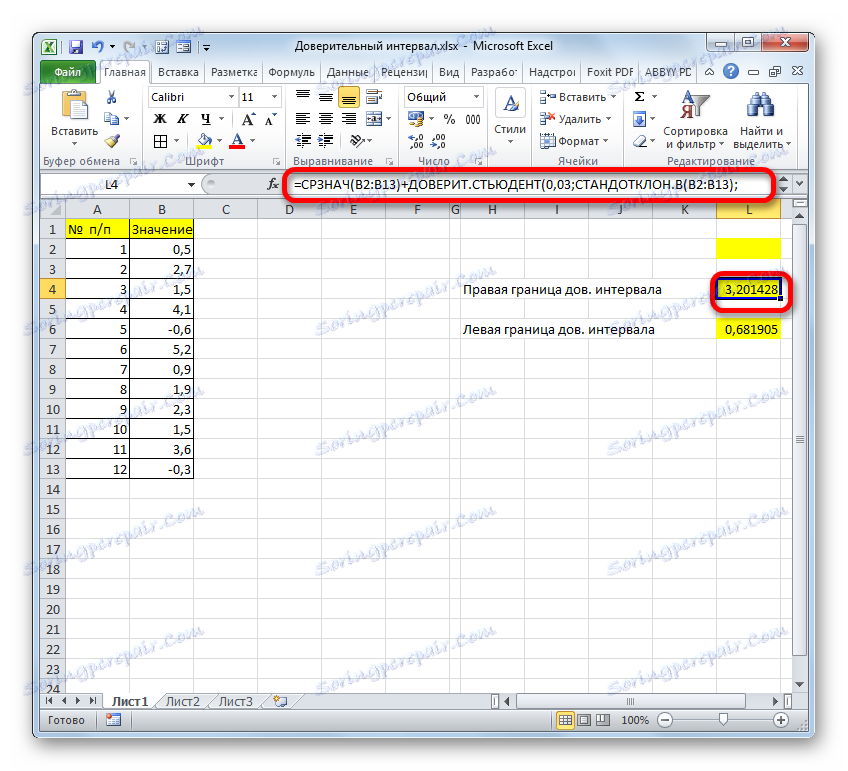
10. با اضافه کردن نتایج محاسبه STEED و STUDENT STUDENT ، ما مرز راست فاصله اطمینان را به دست می آوریم.
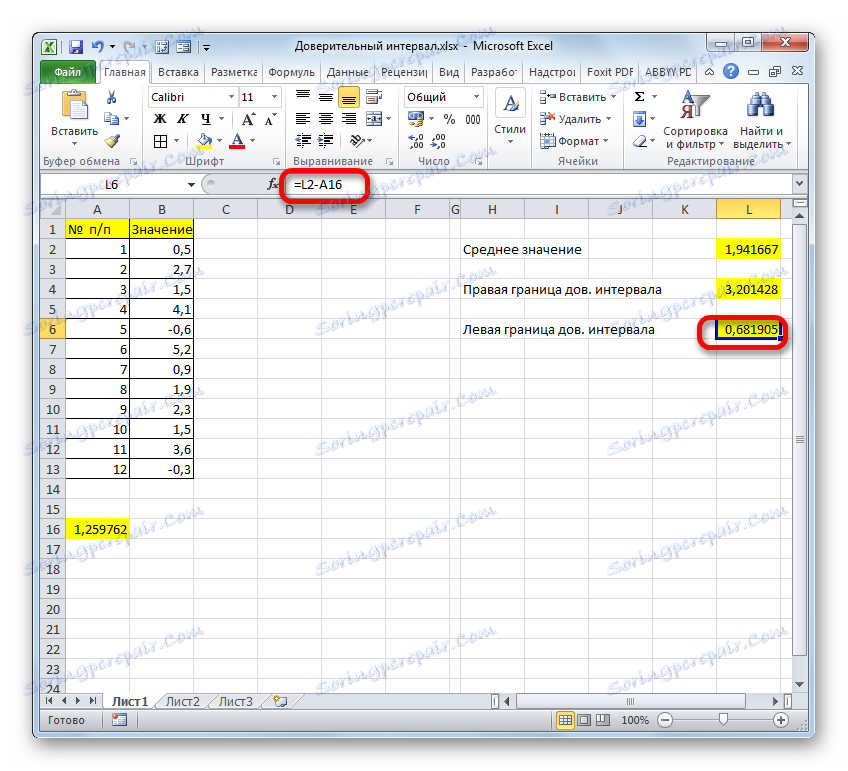
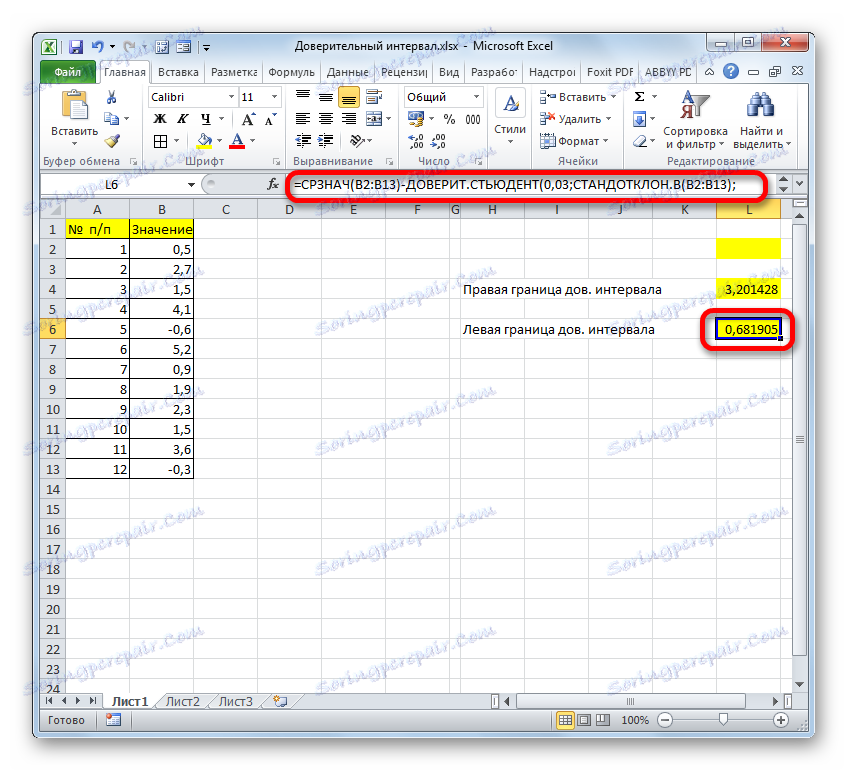
11. پس از برداشت نتیجه محاسبه ی دانشجویان از نتایج محاسبه اپراتور مقدار متوسط ، ما حد چپ فاصله اطمینان را داریم.
12. اگر محاسبه در یک فرمول نوشته شود، محاسبه مرز راست در مورد ما اینگونه خواهد بود:

    =СРЗНАЧ(B2:B13)+ДОВЕРИТ.СТЬЮДЕНТ(0,03;СТАНДОТКЛОН.В(B2:B13);СЧЁТ(B2:B13))

13. بر این اساس، فرمول محاسبه مرز چپ مانند این خواهد بود:

    =СРЗНАЧ(B2:B13)-ДОВЕРИТ.СТЬЮДЕНТ(0,03;СТАНДОТКЛОН.В(B2:B13);СЧЁТ(B2:B13))

همانطور که می بینید، ابزار اکسل به شما اجازه می دهد تا محاسبه فاصله اطمینان و مرزهای آن را به طور قابل توجهی ساده کنید. برای این منظور، اپراتورهای جداگانه برای نمونه هایی که واریانس شناخته شده و ناشناخته است استفاده می شود.

• ← مایکروسافت اکسل رشته تلفیقی
• تبدیل HTML به فرمت مایکروسافت اکسل →